지금까지 우리는 x=0과의 교점, f(x)=0이 되는 x값 Root를 구하기 위한 방법들을 다루어 보았다.이번에는 f(x) 함수 내에서 Max, Min을 만족시키는 Optimal Point를 구하기 위한 방법들을 다루어 볼 것이다.

현재 그려진 그래프에서는 화살표 부분의 Max, Min 부분을 볼 수 있다.
이를 구하기 위한 힌트로는 f(x), f'(x), f''(x)를 이용해서 원하는 값을 찾아내는 것이다.
이는 우리가 5,6,7단원에서 배웠던 Root를 찾는 것과 비슷하다.
접근 Point
위로 볼록한 지점, 아래로 볼록한 지점은
1) f'(x) 값이 0이라는 특징이 있다. 이 점에서 접선을 그었을 때 그 접선 기울기가 0이라는 의미
2) f''(x) 값이 음수라면, 위로 볼록한 그래프, f''(x)가 양수라면 아래로 볼록한 그래프가 그려진다.

앞서 배웠던 내용들은 Root를 찾을 때 사용했던 함수들은 1차원적인 최적화였다.
Max, Min을 다룰 때에는 2차원적인 최적화(가장 최대 지점, 최소 지점)도 이루어진다는 차이점이 있다.
Object function : 최댓값 또는 최솟값을 찾고자 하는 함수를 의미한다. Custom fuction이라고도 한다.
Multi-modal function : 하나이상의 최적점(max, min)이 있는 함수
descriptive : ~을 묘사하다, 기술하다. 어떤 대상을 관찰해보고 표현하는 것.
prescriptive : 아직 대상을 관찰하지 않았지만 먼저 기술을 하는

구간을 어떻게 설정하느냐에 따라서 수없이 많은 local min, max가 존재할 것이다.
실제 우리가 관심을 가지는 것은 Global max, min 또는 구간 내에 가장 크거나 작은 optimal point를 찾는 것이 목표이다.
Ch 13에서 사용하는 함수들에 대한 이름을 먼저 알아보자.
1) Golden-section search (황금 분할 탐색) : Bisection방식과 유사한 방식이다. 수렴하는 특징이 있다.
2) Parabolic interpolation : Golden-section 방법보다 빠르게 수렴할 수도 있지만, 종종 해를 찾지 못하고 발산할 수도 있다.
3) Brent's Method : Hybird Medthod, 조건을 확인해보고 상황에 맞게 함수를 적용해 해를 찾는 방식이다.
Golden-section search
- Golden-section은 unimodal function에서만 사용기 가능, multimodal function일 경우 특정 구간에서만 사용이 가능하다.
타겟 함수의 형태를 알지 못할 때 함수가 Unimodality가 확실한 구간또는 함수일 때, 점들을 비교해서 해가 존재하는 구간을 줄여 나가는 탐색 알고리즘이다.
황금비율을 이용하기 때문에 황금비 탐색이라고 한다.
unimodal function : 하나의 max 또는 min을 가지고 있는 함수
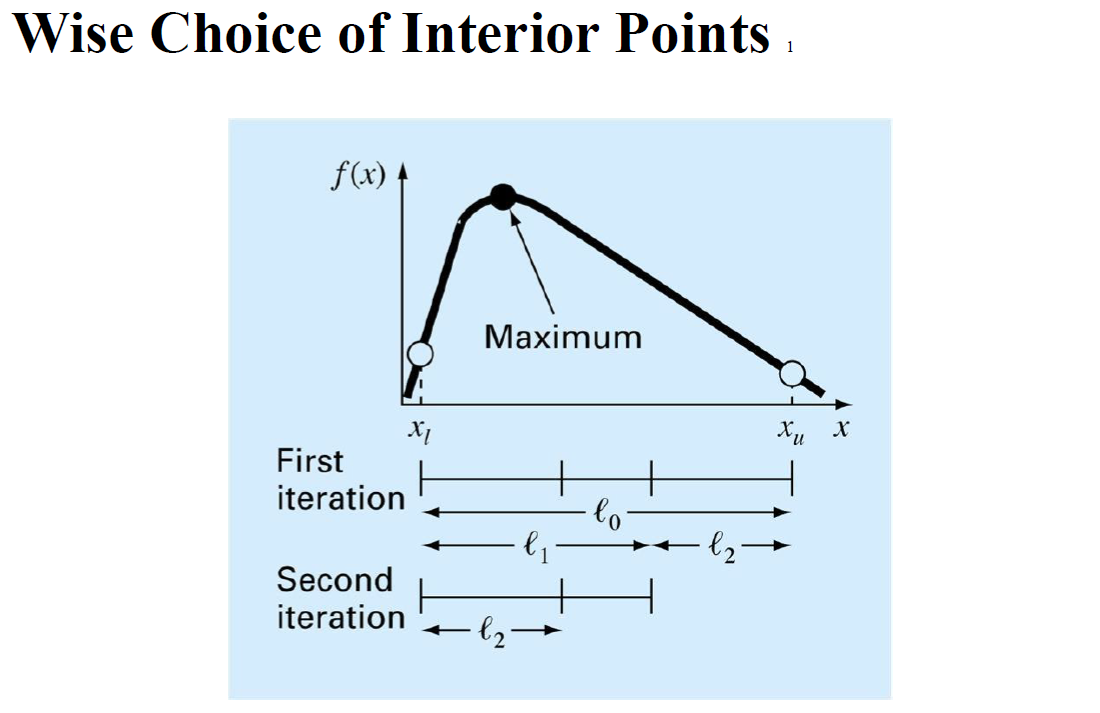
황금비 1.1618... 을 이용하는 함수이다.
전체 길이를 L0라고 하였을 때 길이의 비를 황금비가 되도록 L1, L2로 나눈다.
근인 d를 구하게 되는데 Lower bound에서만큼 d를 더한 값을 x1, Upper bound에서 만큼 d를 뺀 값은 x2
우리가 활용할 수 있는 점은 xu(Upper bound), xl(Lower bound), x1, x2
Key point) 황금비 d = R* L
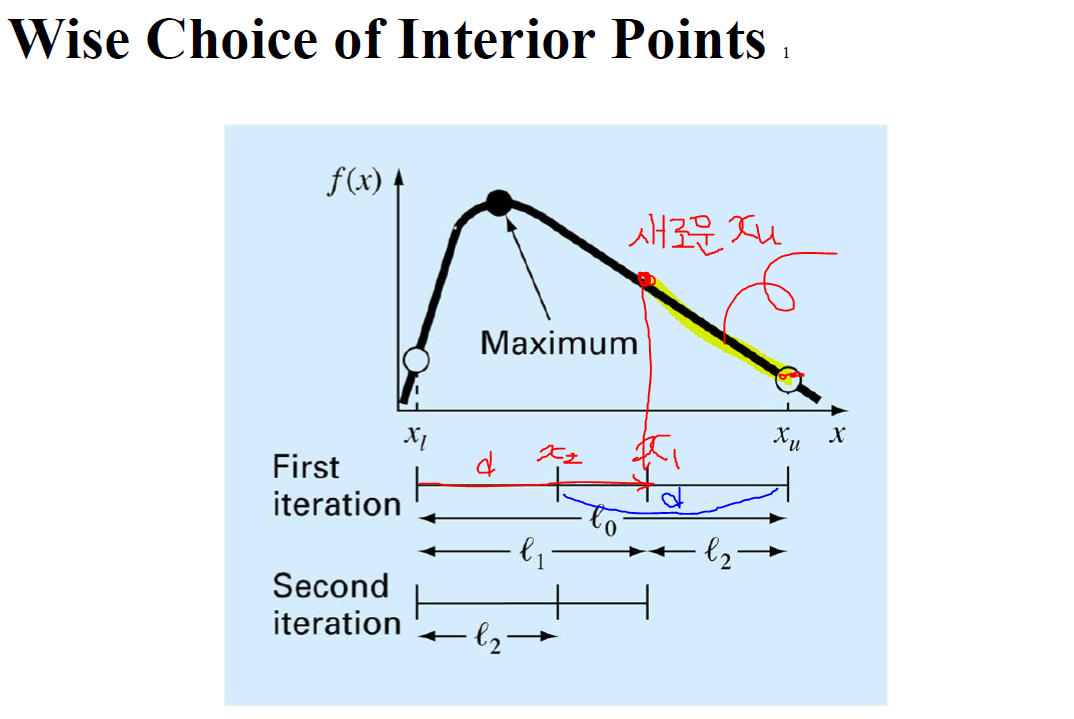
1) 이제 비교를 진행하게 되는데 f(x1)과 f(xu)를 비교하여서 f(xu)가 더 작다면 x1~xu구간은 더 이상 사용하지 않게 된다.
따라서 x1이 새로운 Lower bound가 된다.
이때 새로운 xu가 정해 지더라도 기존에 있던 x2는 x1이 된다.
Lower bound에서 d만큼 더한 값이기도 하며 xu~xl 사이를 황금비로 곱한 값이다. 황금비에 의해서 새로 구하지 않아도 된다.
2) 새로 정해진 xu, xl 사이에서 x1, x2를 구해서 계속해서 optimal point가 있는 지점의 구간을 좁혀 나간다.

R은 0.61803이 나온다. 이 비율을 황금비라고 한다.


가장 중요한 핵심은 d값을 구하는 것인데 황금비율을 이용해서 과정을 반복해 나가는 것이다.
lower bound, upper bound값이 주어졌고 함수도 주어졌으니 우리는 컴퓨터를 이용해 그래프를 먼저 그려본다.

[0,4] 구간에서 unimodal function인 것을 확인할 수 있었다.

L0는 4-0으로 4
d는 R * L0로 2.472
x1 = lower bound + d = 2.472
x2 = upper bound - d = 1.528
f(x1) = 0.63 // f(xu) = -3 -> x1가 새로운 upper bound가 된다.
f(x2) = 1.765 // f(xl) = 0 -> x 2가 새로운 lower bound가 되며, x2는 새롭게 구한다.

Parabolic Interpolation
- Parabolic, 포물선 그래프에서 선을 찍어서 값을 구하고자 하는 알고리즘
세 개의 점을 지나는 2차 함수(포물선 그래프)는 하나만 존재한다.


Parabolic함수는 3개의 점이 주어지고 이 점을 지나는 이차함수를 구해야 한다.

x3를 공식을 이용해서 1.5055 값을 구할 수 있었고, f(x3)의 값은 1.7691이다.
x0, x1, x2 중에서 하나를 버림으로써 구간을 좁히고 과정을 반복해 나간다.

Newton's Method
뉴턴의 개념에서 x(i) 값을 이용해서 x(i+1)를 구하고자 할 때는 다음과 같은 공식을 사용했었다.

optimal 한 값을 구할 때 그 지점은 f'(x) = 0 이므로 활용하게 될 것이다. 위의 식을 응용하여

f(x)에서의 기울기도 접근이 가능한 식으로 활용할 수 있다.

뉴턴의 방정식을 활용하기 위해서는
f'(x)와 f''(x)를 알아야 활용할 수 있다.

이 과정을 이용하게 반복하게 되면


그러나 이 방법은 반드시 수렴한다는 보장이 없고, 만일 미분을 할 수 없는 함수일 경우 활용이 불가능하다.
미분 공식을 사용할 수 없다면 앞에서 다루었던 근사치 값을 이용하여 해결해야 한다.
Brent's Method
- Golden-section search와 parabolic interpolation을 섞어서 사용한다.

Parabolic 방법을 사용할 수 있는지를 먼저 테스트 한번 해보고, 가능하다면 사용하고
그렇지 못하다면 Golden-section을 사용한다.
[Parabolic이 optimal에 접근하는 데에 더 빠르기 때문에 먼저 접근]
'CS_컴퓨터이론 > 수치해석' 카테고리의 다른 글
| [수치해석] 다차원함수 최적화 Multidimensional Unconstrained Optimization (1) | 2022.12.12 |
|---|---|
| [수치해석 / Colab ] Bisection , FalsePosition 슈도코드 프로그래밍 (0) | 2022.11.22 |
| [수치해석 / Colab] 테일러 급수로 자연로그함수 구하기 (0) | 2022.11.20 |
| [수치해석 / Colab] Python프로그래밍 Sin, Cos, 자연로그 함수 테일러 전개 (0) | 2022.11.20 |
| [수치해석] Open Method : Simple Fixed-Point Iteration & The Newton-Raphson Method (0) | 2022.10.23 |