1. 과학기술인으뜸적금
과학기술인으뜸적금이란?
- 회원이 자율적으로 가입금액과, 가입기간을 정하고, 매월 납부하여 목돈을 모으는 정기적금형 상품
가입대상은??
- 과학기술인공제회의 퇴직연금급여사업 및 적립형공제급여사업 가입회원 및 퇴직회원
- 과학기술인공제회법 제6조 및 정관 제 4조에 따른 일반회원 가입자격이 있는사람 (최근 추가된 내용)
가입금액은???
- 월 납입액 : 최소 10만원 ~ 가입한도 범위에서 본인이 선택 ( 1만원 단위 )
- 가입한도 : 전 가입계좌 만기원금 총액 1억원한도
[ 1년 (월 833만원), 2년(월 416만원), 3년(월 277만원), 5년(월 166만원) ]
- 가입한도 내 복수 가입 가능
- 가입기간 중 증감좌 가능(한도범위내증감좌횟수 등 제한없음)
가입기간은????
1년 (12회) / 2년 (24회) / 3년 (36회) / 5년(60회)
회원지급률(일반) : 연 4.50% / 연복리 / 고정금리 (2023년 6월 12일부터)
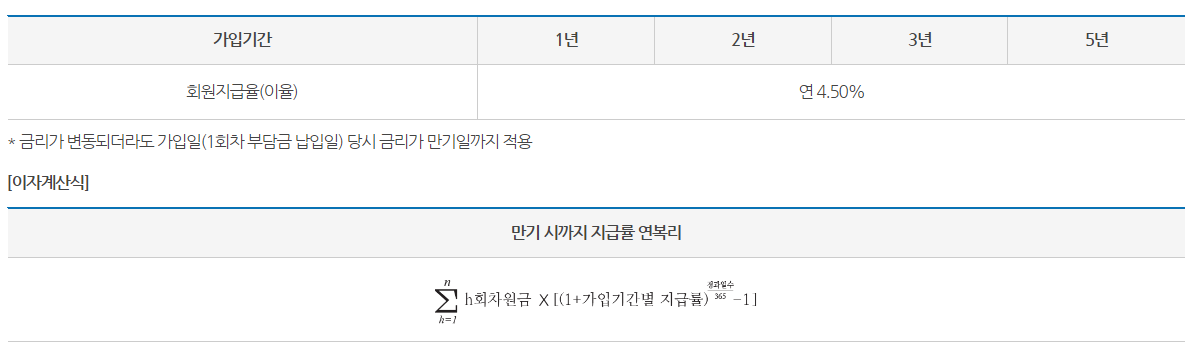
- 기타 세율 및 납부방법, 중도해지 지급률에 관해서는 방문하여 확인해주세요!!
과학기술인공제회
www.sema.or.kr
2. 본인의 상황을 고려하여 상품 가입
▶ 5년(60회) 상품을 선택한 이유는
- 5년 납부후 예상금액을 보고 1,2,3년후 예상금액을 보니 할꺼면 5년으로 해야겠다고 마음 먹었습니다..!!
월 50만원 납부 시 세후 이자
1년(12회) : 121,040원
2년(24회) : 474,790원
3년(36회) : 1,071,400원
5년(60회) : 3,054,680원
납부금액에서도 고민을 많이 하였습니다...
▶ 월 30만원씩 5년을 납부한다면 세후 이자로 약 180만원

▶ 월 50만원씩 5년을 납후한다면 세후이자로 약 300만원

6개월동안 소비패턴을 살펴본 결과 다른 적금상품도 납부중인 저에게...
월 50만원을 납부하는 것은 무리가 있다고 판단하여 월 30만원 납부로 가입하였습니다.!!
하지만 연봉이 오르고, 추가적인 납부가 가능하다면 증액/증감이 가능한것도 이 상품의 장점아니겠습니까
3. 가입절차 및 필요서류


가장 중요한 자격증빙서류를 제출해야합니다!!
자격증빙서류는 다음과 같습니다 ( 발급 기간이 1개월이내만 유효 )

저 같은 경우에 "가입자격 대상기관 재직자"에 해당하여서 3. 국민연금 가입증명서 를 제출하여 증빙하였습니다!
4. 신청이후 승인부터 납부까지
이후 출금이체 동의를 진행하고 상품 가입 신청이 접수되면 카카오톡으로 연락왔습니다!!

2024년 1월 11일 목요일에 신청하여 14일 화요일에 승인되었다는 연락을 받았습니다!
승인 기간은 사람마다 상이하겠지만 일주일 내외인거같습니다.



납입일을 1일로 설정하였기에 다음 달 1일 출금될 예정!
출금 예정시간이 은행별로 상이하므로 출금 전일부터 잔고관리해야합니다!
투자에는 자신이 없었던 제에게 목돈을 마련하기 위해서 5년 적금이 적합하다고 생각하였습니다
5년뒤 행복한 날을 상상하며 포스팅 마무리하도록 하겠습니다!!
'무념무상 일상이야기 > 내돈내산 방문&사용후기' 카테고리의 다른 글
| 서울 안국역 맛집 "런던 베이글 뮤지엄" 방문후기, 웨이팅, 조기마감 (0) | 2022.10.18 |
|---|---|
| 서울 삼각지 맛집 "몽탄" 방문 후기 (0) | 2022.10.12 |